Recently, the team of Professor Kihwan Kim of BAQIS/Tsinghua University has made new progress on error-mitigated quantum computation with trapped ions, demonstrating the ability of suppressing errors in complex quantum circuits without additional quantum resources. On December 7, 2023, this result was published in "npj Quantum Information" under the title "Error-mitigated quantum simulation of interacting fermions with trapped ions".

Numerous efforts have been made to realize useful algorithms beyond the limitation of classical computational capabilitywith noisy intermediate-scale quantum (NISQ) devices. One promising scheme in this direction is to combine the advantages of classical and quantum computers to obtain better computational results than using only classical computers. In this scenario, it is crucial to acquire sufficiently high-precision results of quantum computation without quantum error correction, which is still challenging to realize at a meaningful scale with state-of-the-art systems.

Various methods mitigating errors have been proposed and applied to improve the computation results of quantum devices. However, most mitigation techniques applied in experiments to date were based on certain properties or assumptions on the noise of specific hardware or algorithms. General error-mitigation methods have not been experimentally implemented or tested in a full quantum circuit. Here, error mitigations focusing on the probabilistic error cancellation, the most generic and systematic method were demonstrated with trapped ions as shown in Figure 1. As a benchmark, dynamics of interacting fermions was tested, where the precision of dynamics was increased by close to an order of magnitude through error mitigations.

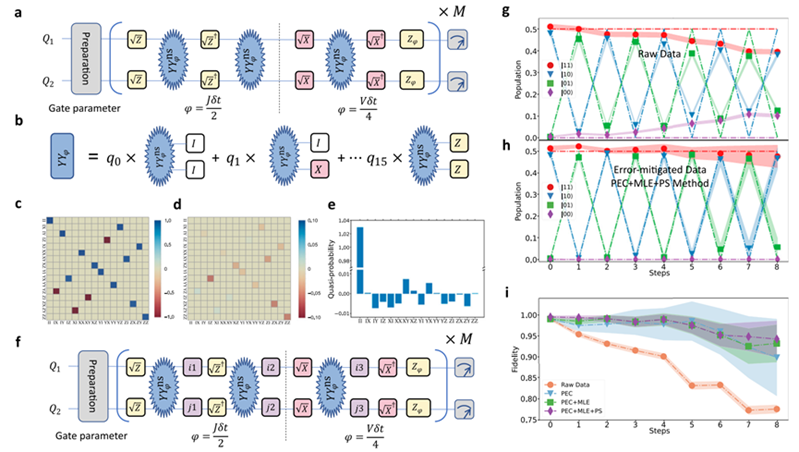
Figure 1. Error-mitigated quantum computation. (a) Quantum circuit of Trotter expansion for the simulation of dynamics of two spinless fermions. (b) Probabilistic error cancellation scheme. (c) Pauli transfer matrix, (d) Deviation of Pauli transfer matrix, and (e) Quasi-probabilities in the decomposition of the inverse error operations for the experimental gate, which is characterized through quantum process tomography. (g) Experimental data and (h) error-mitigated data for V=2J. (i) Population fidelity of experiment data and error-mitigated data

These improvements made it possible to successfully simulate and to observe that the charge and the spin of fermions behave differently as popularly expected in the Fermi-Hubbard model. As an example, in Figure 2, two fermion models containing spin were encoded in a four-ion system, and were simulated without the intra-lattice interaction (Figure 2a-d) and with the intra-lattice interaction. (Figure 2e-h). By extracting the spin and charge distribution (Figure 2d, h), the spin-charge separation of fermions was observed, thus verifying that the error mitigation scheme is effective for long quantum circuits.

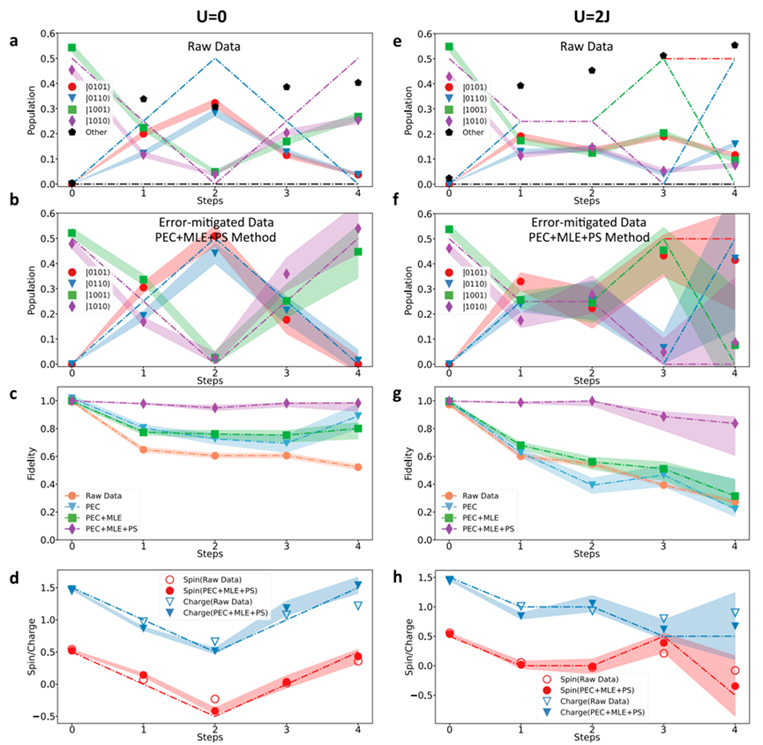
Figure 2. Dynamics of four fermionic modes mapped by two fermion sites and spins. Ouput population with the initial state of (a)–(d) for no interaction U = 0 and (e)–(h) for U = 2J. (a,e) Experimentally measured population without error mitigations and (b,f) with error mitigation. (c,g) The population fidelities after each error-mitigation method as PEC, MLE, and PS. (d,h) Fermionic spin and charge population.

The demonstration can be essential and exemplary to demonstrate algorithms that go beyond classical limitations, such as variational quantum algorithms in which the time evolution of a Hamiltonian inspires the circuit design, using the quantum system in the currently available NISQ regime. The improved results by error-mitigations are also expected to stimulate more practical applications with large-scale implementations.

The first authors of the paper are Chen Wentao, a postdoctoral fellow at Tsinghua University, and Zhang Shuaining, an assistant research at BAQIS and a lecturer at Renmin University. The corresponding authors are Zhang Shuaining, Li Ying, a researcher at the China Institute of Engineering Physics, Zhang Jingning, an associate researcher at BAQIS, and Kihwan Kim. This research was funded by the Quantum Science and Technology Innovation Program and the National Natural Science Foundation of China.

Available at https://www.nature.com/articles/s41534-023-00784-8