On January 29, 2021, a team led by Professor Gui-Lu Long, a jointly appointed researcher at the Beijing Academy of Quantum Information Sciences and a professor at Tsinghua University, published an article on "npj Quantum Information", a nature partner journal, showing further improvement over previously quantum gradient descent algorithm. This enhancement reduces the resource requirements for quantum circuits in previous algorithm, making it feasible to implement using existing quantum systems. It is anticipated that this quantum algorithm may demonstrate advantages over classical algorithms in high-dimensional data optimization problems.

Gradient descent is a cornerstone of traditional numerical optimization and an integral part of numerous machine learning algorithms noweday. The central idea of the gradient descent algorithm is to iteratively evolve the objective function in the direction of the optimal gradient, thereby identifying local minima of the objective function. However, optimizing high-dimensional data poses a substantial computational chanllenge, potentially exceeding the capabilities of current classical computation. To address this challenge, researchers have leveraged the advantages of quantum computing and proposed a quantum version of the gradient descent algorithm. This quantum algorithm employed the quantum phase estimation methods, requiring deep quantum circuits that are hard to achieve due to factors such as quantum gate operation errors.

Professor Gui-Lu Long's team introduced an improved version of the algorithm that utilizes the Linear Combination of Unitaries (LCU) method, which was proposed by Gui-Lu Long, to develop the quantum gradient algorithm. They presented a quantum circuit representation that reduces the number of quantum state copies from a polynomial count to a mere constant, independent of the system size, by significantly reducing the circuit depth. This reduction in quantum gate operations makes it achievable on currently resource-constrained quantum processors. The team demonstrated the improved algorithm for optimizing polynomial problems in a 4-qubit nuclear magnetic resonance system. Using a two-dimensional vector composed of a quantum state of 1 qubit, the algorithm was demonstrated under various initial conditions, achieving a fidelity of over 94% in obtaining local minima through experiments.

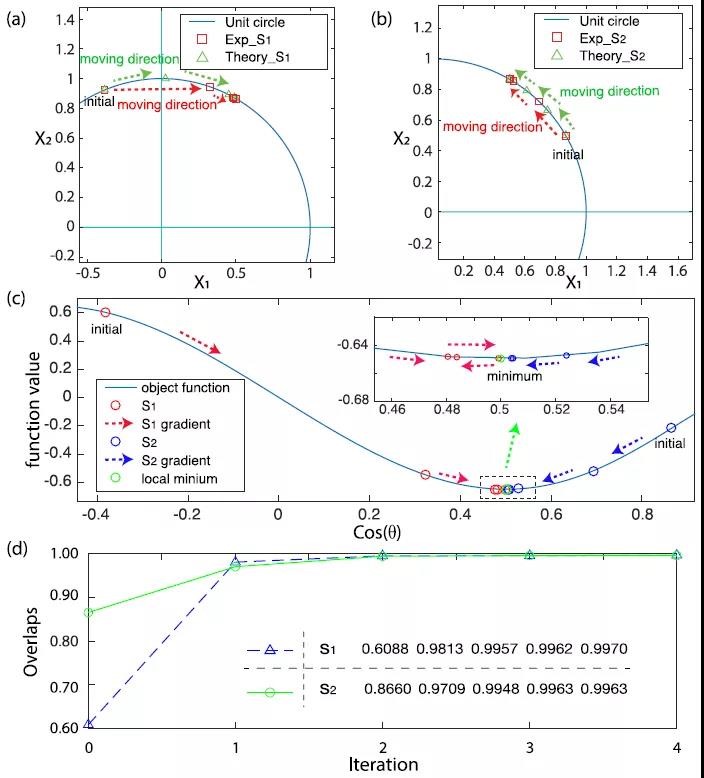
As shown in the figure, starting from different initial points, the quantum gradient descent algorithm successfully converges to the extreme. This algorithm can be directly applied to multidimensional scaling problems in large data analysis. Figures (a), (b), and (c) illustrate the convergence process from different initial points to the extreme. The green and red colors represent theoretical simulations and experimental implementations, respectively. Panel (d) describes the fidelity of the quantum state at each step of the gradient iteration in the experiment.

Considering the advancement of quantum computer hardware, this quantum gradient descent algorithm shows great potential in relevant fields. This work provides a faster solution to high-dimensional optimization problems. Importantly, similar to the full quantum eigenstate solver algorithm constructed by the team using the LCU, this algorithm can not only run on current noisy quantum computing devices but can also be directly used as an application software on future fault-tolerant quantum computers.

Link to the paper：https://doi.org/10.1038/s41534-020-00351-5