Recently, the Cloud Quantum Computing Platform Group at the Beijing Academy of Quantum Information Sciences (BAQIS), in collaboration with the Institute of Physics, Chinese Academy of Sciences (IOP, CAS), Augsburg University in Germany, and RIKEN in Japan, demonstrated a scalable method for probing infinite-temperature spin transport using a ladder-type superconducting quantum processor, and also simulated the diffusion and subdiffusion behavior of spin hydrodynamics on an analog quantum simulator. On August 31, 2024, the corresponding results were published in Nature Communications entitled "Probing spin hydrodynamics on a superconducting quantum simulator."

In the field of classical physics, fluid transport phenomena generally follow the diffusion equation in fluid mechanics, which describes the power-law behavior of the autocorrelation function of fluid density during late-time evolution. The rate of this power-law decay, known as the transport exponent (denoted as α), characterizes the general properties of diffusive motion in fluid mechanics. It has been discovered with further research that similar phenomena to classical fluid mechanics can also occur in the dynamics of microscopic quantum systems. For example, in spin quantum systems, spin observables at infinite temperature mathematically satisfy a diffusion-like equation. Consequently, the long-time evolution of the spin autocorrelation function also exhibits power-law decay characteristic of diffusion. For a quantum system with -dimensions, the transport exponent  for normal diffusion in non-integrable systems equals , while anomalous superdiffusion and subdiffusion correspond to transport exponents greater than and less than , respectively.

Over the past few decades, quantum computing and quantum simulation technologies based on superconducting qubits have made remarkable progress in improving scalability, controllability, and coherence. Leveraging these advancements, researchers have observed several novel phenomena in the nonequilibrium dynamics of quantum many-body systems, such as quantum thermalization, ergodicity breaking, time crystals, and quantum information scrambling. More importantly, on this platform, by sampling Haar-random states (pseudo-random states) generated through random sequences of gate operations, the potential for quantum computing to surpass classical computing, known as "quantum supremacy," has been demonstrated. Recently, a method for measuring infinite-temperature autocorrelation functions based on pseudo-random state measurements has been proposed, which opens up practical possibilities for simulating hydrodynamics using random quantum circuits.

The superconducting quantum processor used in this word is a ladder-type sample consisting of 30 qubits, arranged as two coupled chains, each with 15 qubits, as shown in Figure 1(a). The team had previously used this processor to simulate the quantum Hall effect (Nat. Commun. 14, 5433, 2023). This work was conducted in the laboratory of the Cloud Quantum Computing Platform Group at BAQIS, utilizing up to the leftmost 24 qubits. It was first experimentally demonstrated that, in addition to using digitally-generated pseudo-random circuits, unitary evolution controlled by a time-dependent Hamiltonian can also generate pseudo-random states satisfying the Haar measure and be used to measure infinite-temperature spin correlation functions. The work involved preparing multi-qubit pseudo-random states (Figure 2) by simultaneously applying microwave driving to resonantly interacting qubits and, combined with a specially designed quantum circuit, measured the infinite-temperature spin autocorrelation function to characterize the dynamical properties of spin transport (Figures 1(c) and 1(d)). For normal spin diffusion transport, the results verified the 1/2 power-law decay of the transport exponent (Figure 3). Furthermore, by applying on-site disordered potential to each qubit, the team observed a slowing of the spin autocorrelation function decay (Figure 4(a)). As the disorder strength increased, the system gradually entered the anomalous subdiffusive region, with the transport exponent deviating from  (Figure 4(b)). At high disorder levels, the transport exponent approached zero, indicating the freezing of spin transport and the onset of a disorder-induced many-body localized (MBL) phase. In addition, with the enhancement of a linear potential gradient, the team observed anomalous subdiffusive transport emerging in this “tilted ladder” system (Figure 5). It is worth noting that previous experimental studies on many-body localization (MBL) mainly focused on the dynamics of imbalance. Unlike the power-law decay of imbalance in the Griffiths subdiffusive regime induced by disorder, no experimental evidence supports power-law decay of imbalance in Stark many-body localization caused by a linear potential. By measuring the infinite-temperature spin correlation function, this study provides robust experimental evidence for subdiffusive behavior in Stark systems, attributed to Hilbert-space fragmentation.

This study provides the technical foundation for constructing a “hydrodynamics simulator” using superconducting qubits, paving the way for exploring other intriguing nonequilibrium phenomena through the lens of quantum simulation of hydrodynamic transport. The first authors of the study are Yun-Hao Shi (postdoctoral researcher from IOP, CAS), Zheng-Hang Sun (postdoctoral researcher from Augsburg University, Germany), and Yong-Yi Wang (postdoctoral researcher from RIKEN, Japan). The corresponding authors are Heng Fan (researcher of IOP, CAS and jointly appointed researcher of BAQIS), associate researcher Kai Xu (IOP, CAS), deputy chief engineer Zhongcheng Xiang (IOP, CAS), and assistant researcher Kaixuan Huang (BAQIS). Researchers Haifeng Yu (BAQIS) and Guangming Xue (BAQIS) also participated in this work, providing assistances in the Josephson parametric amplifier development. Additional contributors include researcher Dongning Zheng (IOP, CAS), associate researcher Xiaohui Song (IOP, CAS), Professor Yu-Ran Zhang (South China University of Technology), Professor Jieci Wang (Hunan Normal University), as well as BAQIS members Zheng-An Wang (assistant researcher), Kui Zhao (postdoctoral researcher), and Hao Li (postdoctoral researcher). This work was supported by grants from the National Natural Science Foundation of China, the Ministry of Science and Technology Key Projects, the Beijing Natural Science Foundation, and the China Postdoctoral Science Foundation.

Link: https://www.nature.com/articles/s41467-024-52082-2.

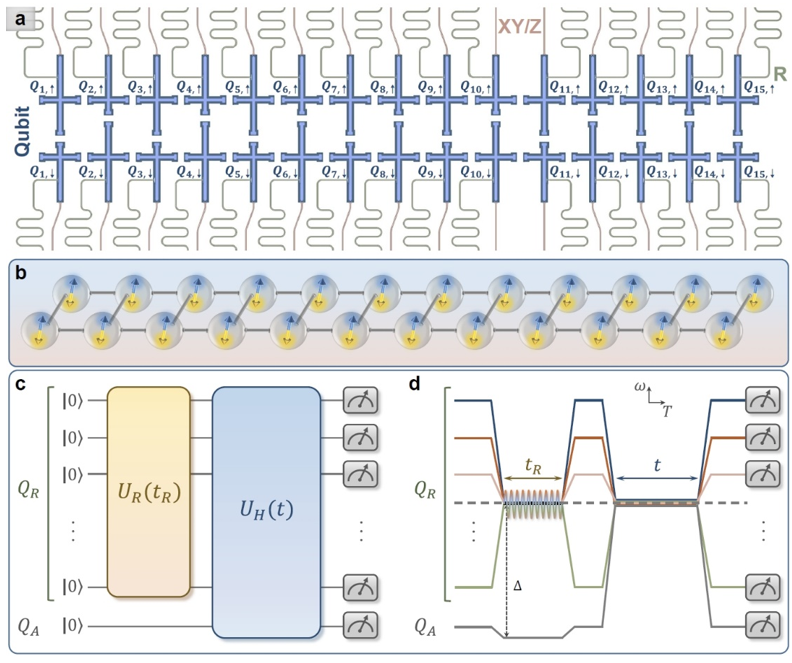
Figure 1: Superconducting quantum simulator and experimental pulse sequences. (a) The schematic showing the ladder-type superconducting quantum simulator, consisting of 30 qubits (the blue region). (b) Schematic diagram of the simulated 24 spins coupled in a ladder. (c) Schematic diagram of the quantum circuit for measuring the autocorrelation functions at infinite temperature. (d) Experimental pulse sequences corresponding to the quantum circuit in (c) displayed in the frequency (ω) versus time (T) domain.

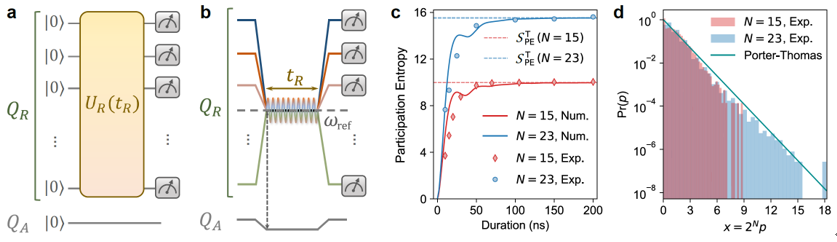
Figure 2: Generation and characterization of the XY drive approach to prepare the Haar-random states. (a) The schematic diagram of the quantum circuit. (b)The corresponding experimental pulse sequence. (c)The evolution of participation entropy SPE vs. the duration of XY drive. The dashed line represents the participation entropy of N-qubit Haar-random state. (d)The bitstring histogram of the measured D=2^N joint probabilities. The solid line shows the ideal results of Poter-Thomas distribution.

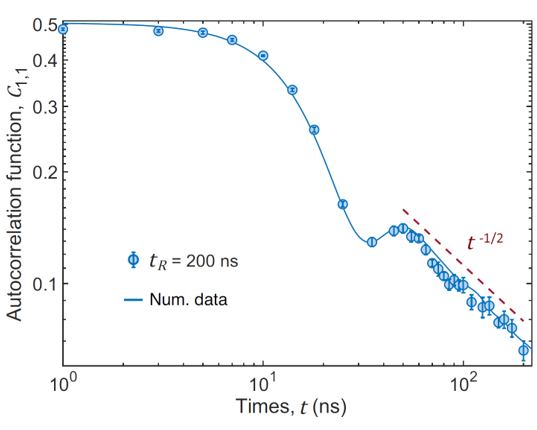
Figure 3: Observation of diffusive transport.

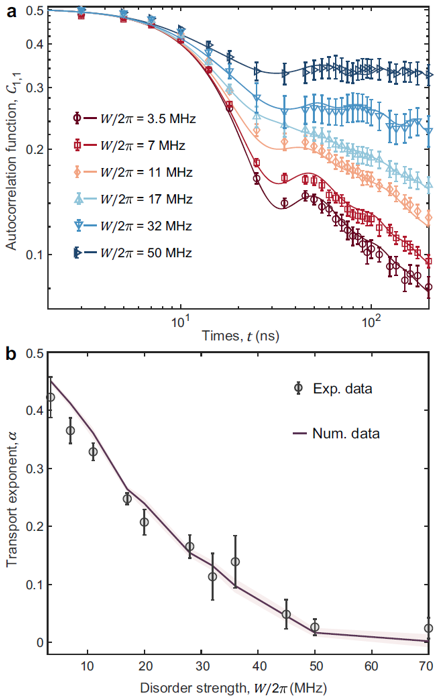
Figure 4: Subdiffusive transport on the superconducting qubit ladder with L=12 disorder. (a)The time evolution of autocorrelation function for the qubit ladder with  and different values of disorder strength W. (b) Transport exponent α as a function of disorder strength  W

Figure 5: Subdiffusive transport on the superconducting qubit ladder with linear potential. (a-b) Time evolution of autocorrelation function for the tilted qubit ladder with different tilted potentials. (c) Transport exponent α as a function of tilted potential.